この記事は、対数価格とは何か?を理解するために書いた記事です。
対数価格とは
対数価格の説明を他サイトで見てみます。
TraidingView の説明です。
TradingView 「対数チャートのご利用方法と重要な理由」
Yahoo ファイナンスにも記載があります。対数 でサーチしてみてください。
チャートの使い方
株価の対数価格の増減は正規分布に従う
株価の変動が対数正規分布する とのことです。
こちらも他サイトでご確認ください。
野村證券 証券用語解説集 正規分布
FXcoin 「リターンの算出をめぐるパラドックス」
対数価格の増減の分布図を描く
株価の対数価格の増減が正規分布に従う ということは、対数価格の増減の分布図を作成すれば、ボラティリティ=リスク が分かるということでしょうか。
リスク は オポチュニティ でもあるので、株価の上昇幅も予測できるようになるのでしょうか。
対数株価の増減の分布図を作成してみます。
バリエーションを見るために、トヨタ自動車 (7203) と チェンジ (3962) の株価を使います。
株価の期間は5年間とします。
株価チャートと対数チャート
株価のデータを pandas-datareader を使って取得します。
ここで株価の対数価格を算出しておきます。
from pandas_datareader.yahoo.daily import YahooDailyReader
date_start = pd.to_datetime('2017-06-29 12:00:00', utc=True)
date_end = pd.to_datetime('2022-06-29 12:00:00', utc=True)
symbols = {
'7203': {'name': 'TOYOTA'},
'3962': {'name': 'CHANGE'},
}
for symbol in symbols:
df = YahooDailyReader(
symbols = symbol + '.T',
start = date_start,
end = date_end,
).read()
# 調整後終値の対数価格を算出する。
df['Adj Close Logarithm'] = df['Adj Close'].apply(np.log1p)
# 株価データを変数に保存する。
symbols[symbol].update({'data': df})
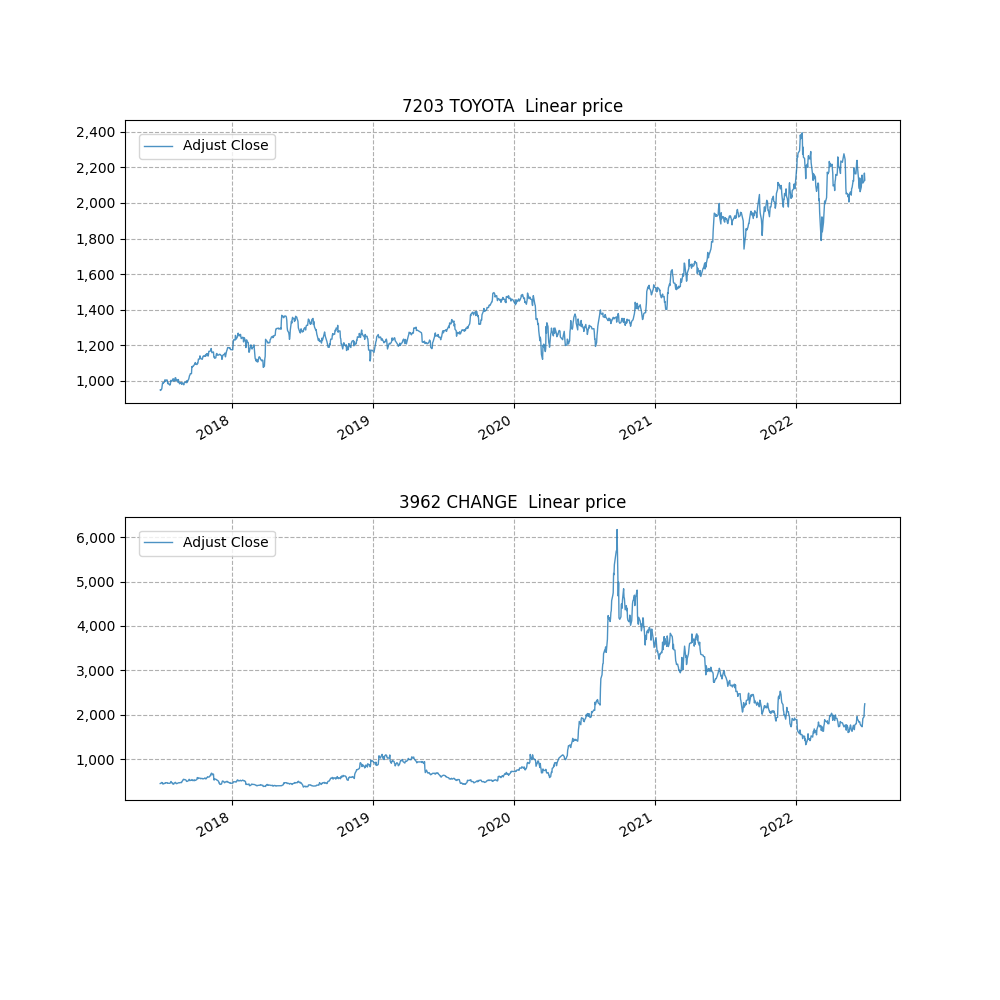
株価チャートを描画してみます。
# 株価チャートを描く。
fig, axes = plt.subplots(len(symbols), 1, figsize=(10, 10))
fig.subplots_adjust(hspace=0.4)
for symbol in symbols:
graph_id = list(symbols.keys()).index(symbol)
name = symbols[symbol]['name']
df = symbols[symbol]['data']
df['Adj Close'].plot(
ax=axes[graph_id],
alpha=0.8,
linewidth=1,
label='Adjust Close',
)
axes[graph_id].set_axisbelow(True)
axes[graph_id].grid(axis='both', linestyle='--')
axes[graph_id].legend(loc="upper left", bbox_to_anchor=(0, 1), borderaxespad=1)
axes[graph_id].set_title('{} {} Linear price' .format(symbol, name))
axes[graph_id].xaxis.label.set_visible(False)
axes[graph_id].yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc:"{:,.0f}".format(x)))
plt.show()
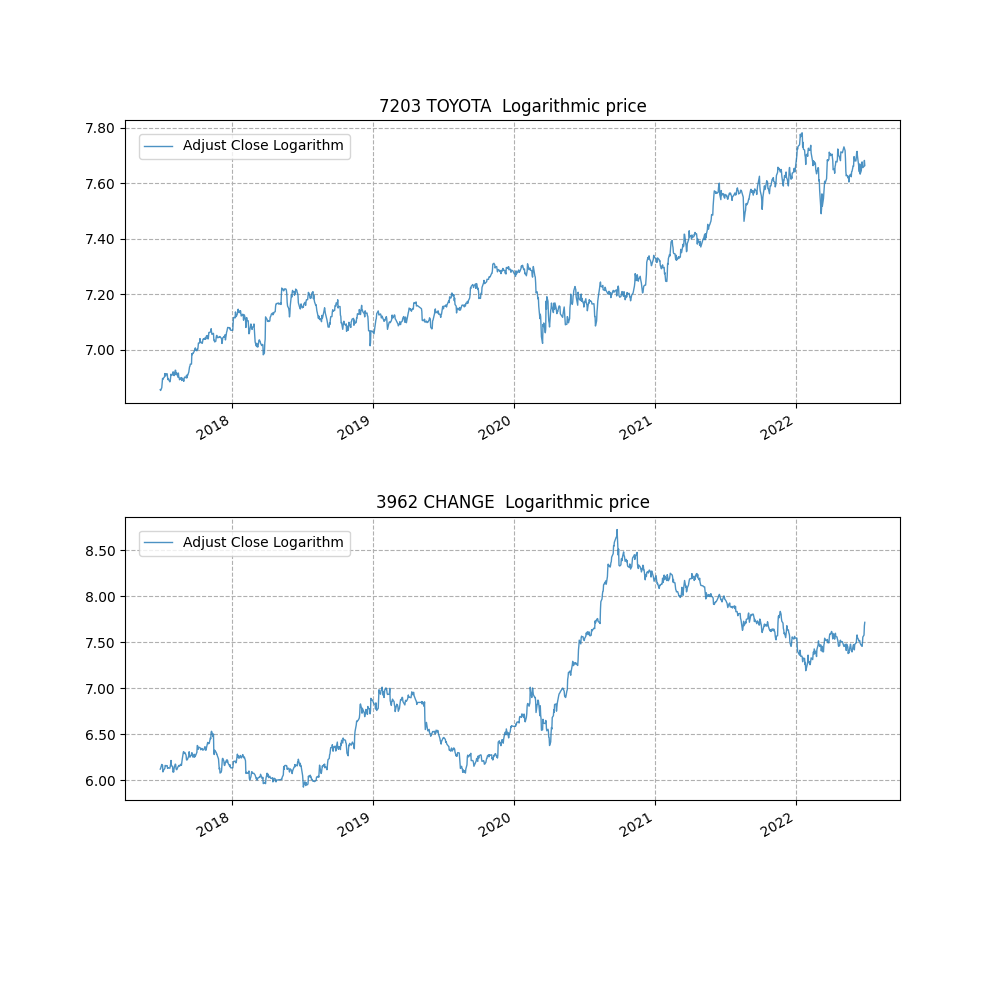
対数チャートを描画します。
株価の対数価格は算出済みなので、描画するのみです。
# 対数チャートを描く。
fig, axes = plt.subplots(len(symbols), 1, figsize=(10, 10))
fig.subplots_adjust(hspace=0.4)
for symbol in symbols:
graph_id = list(symbols.keys()).index(symbol)
name = symbols[symbol]['name']
df = symbols[symbol]['data']
df['Adj Close Logarithm'].plot(
ax=axes[graph_id],
alpha=0.8,
linewidth=1,
label='Adjust Close Logarithm',
)
axes[graph_id].set_axisbelow(True)
axes[graph_id].grid(axis='both', linestyle='--')
axes[graph_id].legend(loc="upper left", bbox_to_anchor=(0, 1), borderaxespad=1)
axes[graph_id].set_title('{} {} Logarithmic price' .format(symbol, name))
axes[graph_id].xaxis.label.set_visible(False)
axes[graph_id].yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc:"{:,.2f}".format(x)))
plt.show()
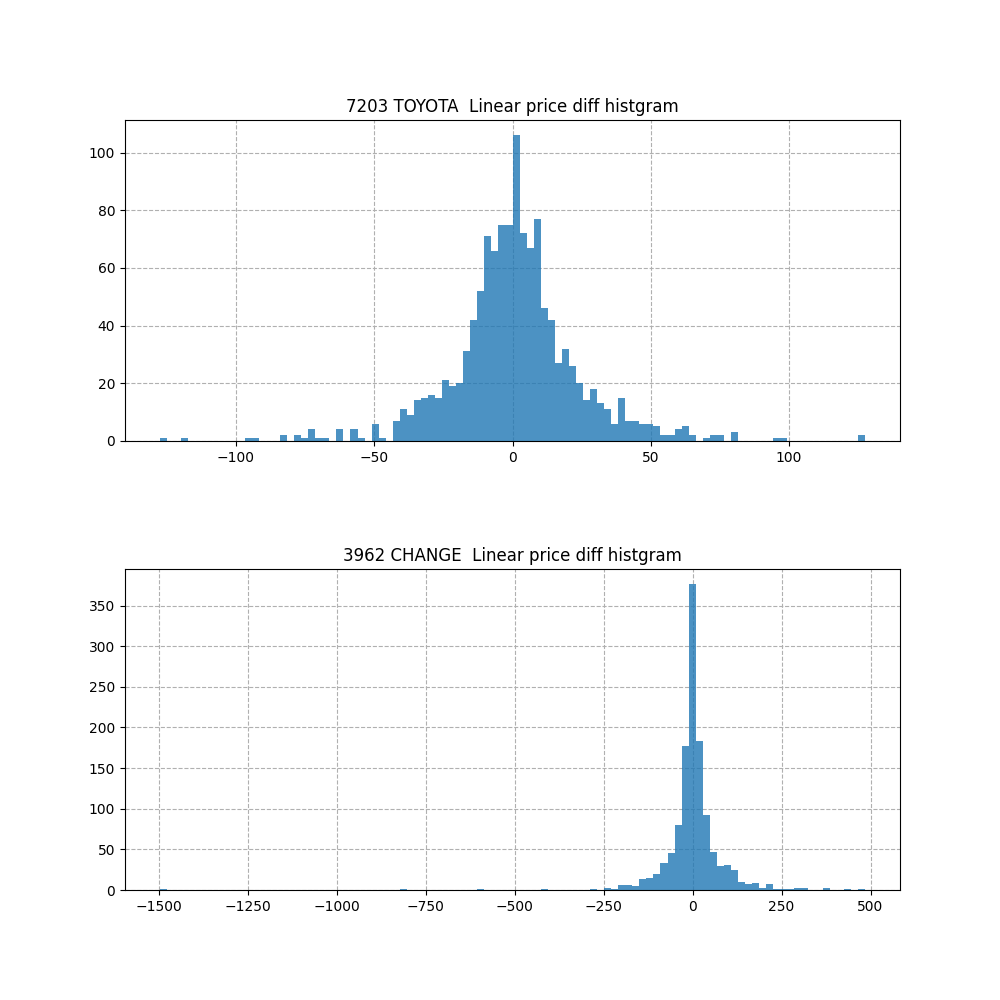
株価と対数価格の増減のヒストグラム
株価の前日からの増減のヒストグラムを描画します。
トヨタ自動車の株価は、5年間で 1,000円 から 2,200円 ぐらいに伸びていますが、株価が安定しているので、株価の変動でも正規分布してそうです。
一方、チェンジの株価は、5年間の中でテンバガーも達成しているので、N% の変動額が時期によって変わるので、ヒストグラムは正規分布しているかもしれませんが、若干細長いものになっています。
# 株価の前日からの増減のヒストグラムを作成する。
fig, axes = plt.subplots(len(symbols), 1, figsize=(10, 10))
fig.subplots_adjust(hspace=0.4)
for symbol in symbols:
graph_id = list(symbols.keys()).index(symbol)
name = symbols[symbol]['name']
df = symbols[symbol]['data']
df['Adj Close'].diff(1).fillna(0).hist(
ax=axes[graph_id],
alpha=0.8,
bins=100,
)
axes[graph_id].set_axisbelow(True)
axes[graph_id].grid(axis='both', linestyle='--')
axes[graph_id].set_title('{} {} Linear price diff histgram' .format(symbol, name))
axes[graph_id].xaxis.label.set_visible(False)
axes[graph_id].yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc:"{:,.0f}".format(x)))
plt.show()
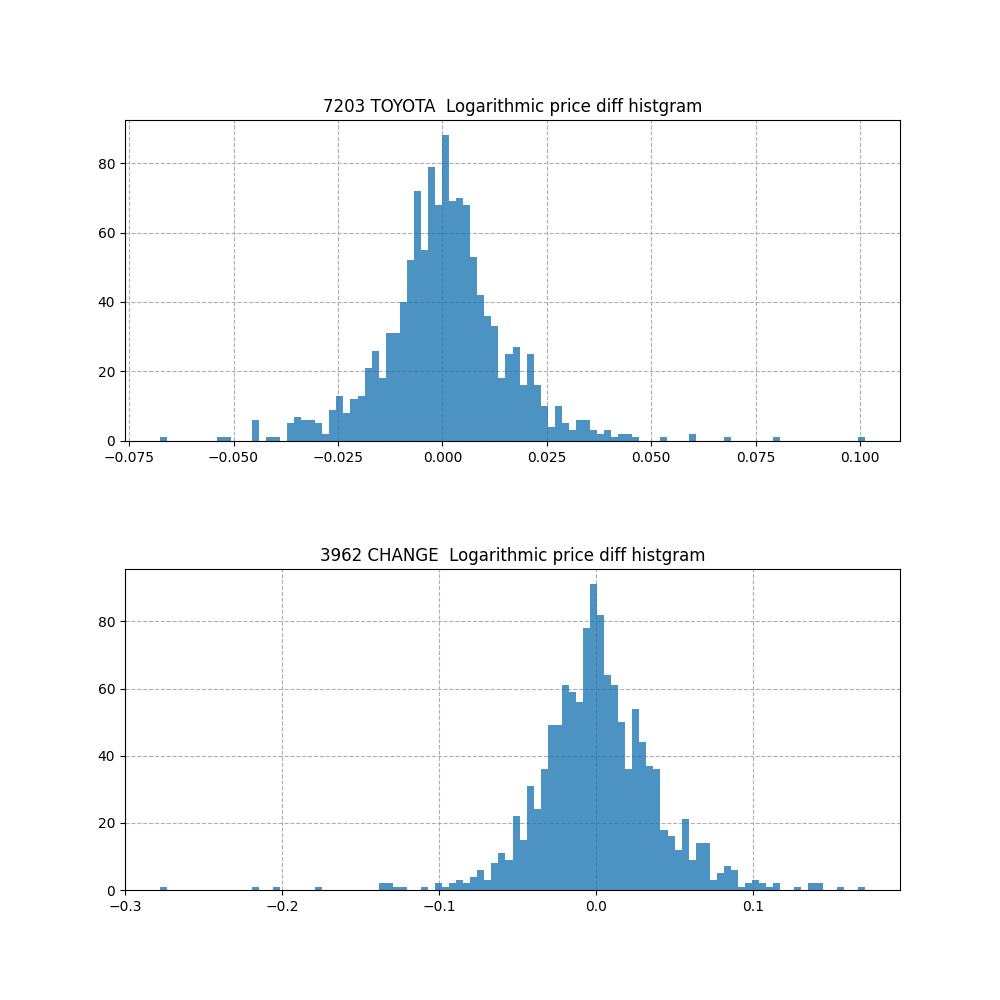
対数価格の前日からの増減のヒストグラムを描画します。
こちらは、トヨタ自動車もチェンジも正規分布してそうです。
2例しか見ていませんが、長期の株価や大きく上下している株価のボラティリティを正しく判断できるのは、対数価格なのではないでしょうか。
# 株価の対数価格の前日からの増減のヒストグラムを作成する。
fig, axes = plt.subplots(len(symbols), 1, figsize=(10, 10))
fig.subplots_adjust(hspace=0.4)
for symbol in symbols:
graph_id = list(symbols.keys()).index(symbol)
name = symbols[symbol]['name']
df = symbols[symbol]['data']
df['Adj Close Logarithm'].diff(1).fillna(0).hist(
ax=axes[graph_id],
alpha=0.8,
bins=100,
)
axes[graph_id].set_axisbelow(True)
axes[graph_id].grid(axis='both', linestyle='--')
axes[graph_id].set_title('{} {} Logarithmic price diff histgram' .format(symbol, name))
axes[graph_id].xaxis.label.set_visible(False)
axes[graph_id].yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc:"{:,.0f}".format(x)))
plt.show()
対数とは
ここまでで、株価の対数価格は使えそうな感じが出てきましたが、”対数価格の変動の 2シグマ は 0.5 です。” とかいわれても、意味がわからないです。
対数価格を普通の株価に戻す方法を調査したいと思います。
そのためには、対数 という言葉を理解する必要がありそうです。
対数 で検索すると、いろいろ出てくるので、そちらをご覧ください。例えば下記サイトなどです。
対数とは何なのかとその公式・メリットについて。対数をとるとはどういう意味か?
上のコードで対数を計算するために、numpy の log1p を使用していますが、その説明は下記サイトをご覧ください。
【NumPy入門 np.log】np.arrayの対数を計算する関数4つを紹介
対数とは、こういうことのようです。
- 24 = 16
- 2 を 4乗 すると 16 になる
- 2 を底とする 16 の対数は 4 である
- log216 = 4
今回使用しているのは、e を底とする対数 = 自然対数 です。
株価の自然対数 = loge株価 です。
トヨタ自動車の例を見てみましょう。株価の自然対数をコードで算出します。
2022/6/29日の終値: 2,128円
2022/6/30日の終値: 2,100円
import numpy as np prices = np.array([2128, 2100]) print(prices) print(np.diff(prices)) # [2128 2100] # [-28] print(np.log1p(prices)) print(np.diff(np.log1p(prices))) # [7.66340766 7.6501687 ] # [-0.01323896]
こうなります。
| 終値 | 終値の自然対数 | |
|---|---|---|
| 2022/06/29 | 2,128円 | 7.66340766 |
| 2022/06/30 | 2,100円 | 7.6501687 |
| 前日との差 | -28円 | -0.01323896 |
対数価格 7.66340766 を株価に戻してみましょう。
- loge[株価] = 7.66340766
- e を底とする [株価] の対数は 7.66340766 である
- e を 7.66340766 乗すると、[株価] になる
- e7.66340766 = [株価]
対数価格の株価の算出式が判明しました。
ネイピア数 math.e を 対数価格 でべき乗すれば、株価に戻せる ことがわかりました。
import math print(math.e) print(math.pow(math.e, 7.66340766)) print(math.pow(math.e, 7.6501687)) # 2.718281828459045 # 2128.999989581781 # 2100.999998224653
対数価格の標準偏差
では、トヨタ自動車 と チェンジ の株価の対数価格の標準偏差を算出してみましょう。
そして、前日の株価の対数価格 + 1シグマ あたりの株価になっているか、確認してみましょう。
for symbol in symbols:
name = symbols[symbol]['name']
df = symbols[symbol]['data']
# 対数価格の前日からの増減の標準偏差を算出する。
sigma = df['Adj Close Logarithm'].diff(1).fillna(0).std()
print('{}: 対数価格の増減の標準偏差 = {:.6f}' .format(name, sigma))
print('{}: {} の終値の対数価格 + 標準偏差 = {:.6f}'
.format(
name,
df.index[-2].strftime('%Y/%m/%d'),
df.at[df.index[-2], 'Adj Close Logarithm'] + sigma,
))
print('{}: {} の終値の対数価格 + 標準偏差 を株価へ変換 = {:,.2f}円'
.format(
name,
df.index[-2].strftime('%Y/%m/%d'),
math.pow(math.e, df.at[df.index[-2], 'Adj Close Logarithm'] + sigma),
))
print('{}: {} の終値 = {:,}'
.format(
name,
df.index[-1].strftime('%Y/%m/%d'),
df.at[df.index[-1], 'Adj Close'],
))
結果です。
TOYOTA: 対数価格の増減の標準偏差 = 0.014988 TOYOTA: 2022/06/28 の終値の対数価格 + 標準偏差 = 7.696779 TOYOTA: 2022/06/28 の終値の対数価格 + 標準偏差 を株価へ変換 = 2,201.25円 TOYOTA: 2022/06/29 の終値 = 2,128.0 CHANGE: 対数価格の増減の標準偏差 = 0.038534 CHANGE: 2022/06/28 の終値の対数価格 + 標準偏差 = 7.719633 CHANGE: 2022/06/28 の終値の対数価格 + 標準偏差 を株価へ変換 = 2,252.13円 CHANGE: 2022/06/29 の終値 = 2,249.0
それっぽい感じになってそうです。
なんとなく 対数価格 がわかってきました。