お困りの方へ
棒グラフや散布図を描いたら、近似曲線を付け足したくなりますよね?
この記事では、グラフの多項式近似曲線の書き方を説明します。
前準備
インポートするモジュール
この記事で示すサンプルコードに必要なモジュールは以下です。
import pandas as pd import numpy as np import matplotlib.pyplot as plt
グラフにするデータの用意
グラフに使うデータをpandas.DataFrameで用意します。
# グラフのデータ作成
df = pd.DataFrame(
data=[2, 10, 6, 30, 85, 70],
index=[0, 1, 2, 3, 4, 5],
columns=['apple'],
)
print(df)
# apple
# 0 2
# 1 10
# 2 6
# 3 30
# 4 85
# 5 70
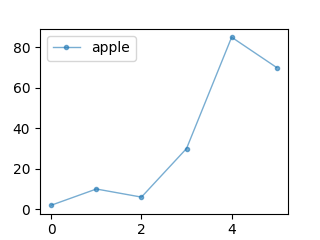
上記グラフを描くコードです。
fig, ax = plt.subplots(1, 1, figsize=(3.2, 2.4))
df['apple'].plot(
ax=ax,
linewidth=1,
alpha=0.6,
marker='.',
label='apple',
)
ax.legend() # 凡例の表示
plt.show()
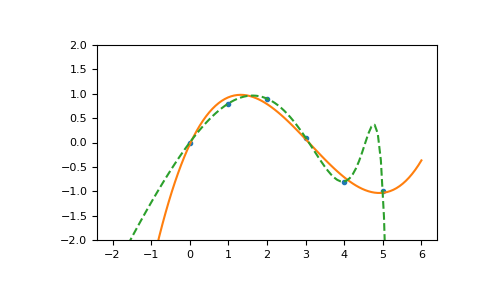
numpy.polyfitを理解する
numpy.polyfitは、与えられたデータに対して、指定された次数の多項式曲線をフィットさせる関数です。
近似式を算出する
では、用意したデータの多項式近似曲線を算出します。
1次近似直線
元データのプロットする点(x, y)のリストと次数(1)をnumpy.polyfitに渡すと、近似直線の傾きとY切片が返ってきます。
近似直線は y = 16.82857143 * x – 8.23809524 となりました。
# X軸の値のnumpy.ndarrayを作成する。 x = np.array(df.index.tolist()) print(x) print(type(x)) # [0 1 2 3 4 5] # <class 'numpy.ndarray'> # Y軸の値のnumpy.ndarrayを作成する。 y = np.array(df.values.reshape(1, 6)[0]) print(y) print(type(y)) # [ 2 10 6 30 85 70] # <class 'numpy.ndarray'> # 近似直線の算出 p1 = np.polyfit(x, y, 1) print(p1) print(type(p1)) # [16.82857143 -8.23809524] # <class 'numpy.ndarray'>
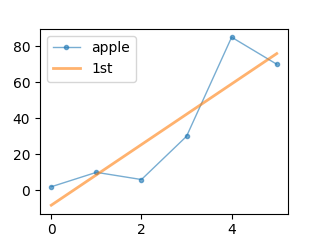
上記グラフを描くコードです。
fig, ax = plt.subplots(1, 1, figsize=(3.2, 2.4))
df['apple'].plot(
ax=ax,
linewidth=1,
alpha=0.6,
marker='.',
label='apple',
)
# 近似直線のYの値を算出する。
y1 = p1[0] * x + p1[1]
# 近似直線を描く。
ax.plot(
x,
y1,
linewidth=2,
alpha=0.6,
label='1st',
)
ax.legend() # 凡例の表示
plt.show()
2次の近似曲線
元データのプロットする点(x, y)のリストと次数(2)をnumpy.polyfitに渡すと、近似曲線の2次方程式のパラメータが返ってきます。
近似曲線は y = 2.16071429 * x2 + 6.025 * x – 1.03571429 となりました。
# 2次の近似曲線の算出 p2 = np.polyfit(x, y, 2) print(p2) print(type(p2)) # [ 2.16071429 6.025 -1.03571429] # <class 'numpy.ndarray'>
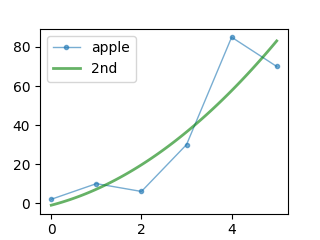
上記グラフを描くコードです。
fig, ax = plt.subplots(1, 1, figsize=(3.2, 2.4))
df['apple'].plot(
ax=ax,
linewidth=1,
alpha=0.6,
marker='.',
label='apple',
)
# 曲線を滑らかにするために、X軸の値を増やす。
xnew = np.linspace(x[0], x[-1], 100)
# 2次の近似曲線の値を算出する。
y2 = p2[0] * xnew**2 + p2[1] * xnew + p2[2]
# 2次の近似曲線を描く。
ax.plot(
xnew,
y2,
linewidth=2,
alpha=0.6,
color='green',
label='2nd',
)
ax.legend() # 凡例の表示
plt.show()
3次の近似曲線
元データのプロットする点(x, y)のリストと次数(3)をnumpy.polyfitに渡すと、近似曲線の3次方程式のパラメータが返ってきます。
近似曲線は y = – 2.60185185 * x3 + 21.67460317 * x2 – 29.62037037 * x + 6.76984127 となりました。
# 3次の近似曲線の算出 p3 = np.polyfit(x, y, 3) print(p3) print(type(p3)) # [ -2.60185185 21.67460317 -29.62037037 6.76984127] # <class 'numpy.ndarray'>
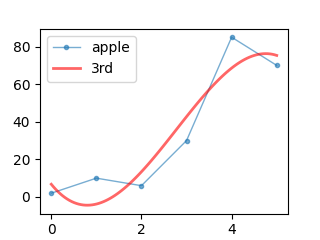
上記グラフを描くコードです。
fig, ax = plt.subplots(1, 1, figsize=(3.2, 2.4))
df['apple'].plot(
ax=ax,
linewidth=1,
alpha=0.6,
marker='.',
label='apple',
)
# 曲線を滑らかにするために、X軸の値を増やす。
xnew = np.linspace(x[0], x[-1], 100)
# 3次の近似曲線の値を算出する。
y3 = p3[0] * xnew**3 + p3[1] * xnew**2 + p3[2] * xnew + p3[3]
# 3次の近似曲線を描く。
ax.plot(
xnew,
y3,
linewidth=2,
alpha=0.6,
color='red',
label='3rd',
)
ax.legend() # 凡例の表示
plt.show()