時系列データを扱う際には、定常性を意識して特徴量を設計することが重要です。
出典:株式分析チュートリアル | 日本取引所グループ
定常性
定常性 とは何でしょうか?
いろいろ検索してみましたが、難しい説明が多く、簡単な説明はありませんでした。
漢字から紐解くと、時間方向に依存せず、安定している状態 みたいな性質でしょうか。
weblio辞書 では、定常とは「一定していて変わらないこと」でした。
この記事では、時系列データに定常性を持たせる ことをやってみたいと思います。
定常性を持った特徴量を生成できるようになり、その特徴量で学習した価格予測の機械学習モデルの精度が上がるようにしたいと思います。
参考にしたサイトを載せておきます。
時系列データに対する3つの特徴把握方法(変動成分・定常性・コレログラム)
非定常な時系列データを変換して定常性を持たせる解析
今回使用するモジュールは statsmodels です。
statsmodels 公式ドキュメント
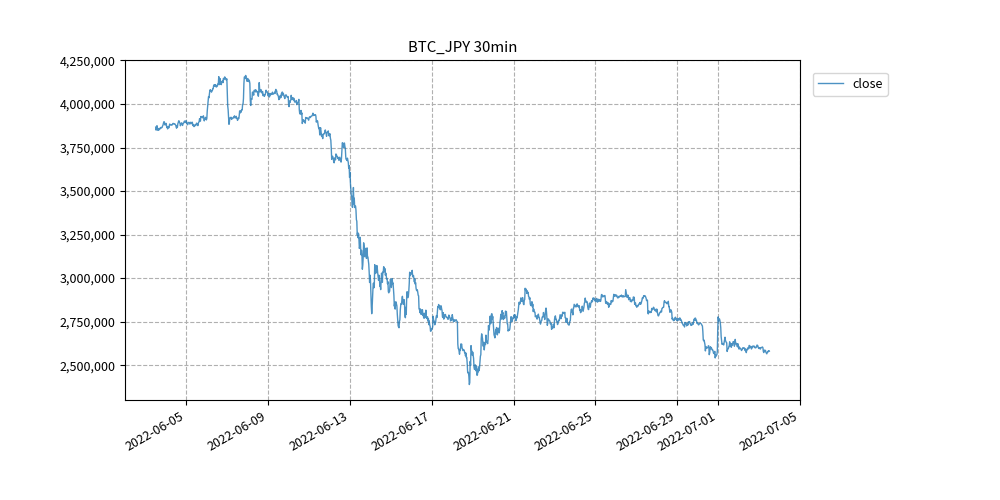
時系列データは、この記事で紹介したBTC 30分足を使います。
 ビットコインのOHLCVデータを生成する
ビットコインのOHLCVデータを生成する
open high low close volume timestamp 2022-06-03 12:00:00+00:00 3871158.0 3878715.0 3859727.0 3867432.0 92.52 2022-06-03 12:30:00+00:00 3867771.0 3892600.0 3843685.0 3849837.0 215.61 2022-06-03 13:00:00+00:00 3850998.0 3872485.0 3838975.0 3858000.0 161.69 2022-06-03 13:30:00+00:00 3857271.0 3883537.0 3853220.0 3875389.0 159.31 2022-06-03 14:00:00+00:00 3875667.0 3881750.0 3852408.0 3856946.0 88.79 ... ... ... ... ... ... 2022-07-03 10:00:00+00:00 2572305.0 2580085.0 2570074.0 2576821.0 47.99 2022-07-03 10:30:00+00:00 2576821.0 2583000.0 2574000.0 2576248.0 37.11 2022-07-03 11:00:00+00:00 2576134.0 2585896.0 2574825.0 2583192.0 29.33 2022-07-03 11:30:00+00:00 2583100.0 2584224.0 2578557.0 2579012.0 23.79 2022-07-03 12:00:00+00:00 2579000.0 2582305.0 2578145.0 2580562.0 20.73
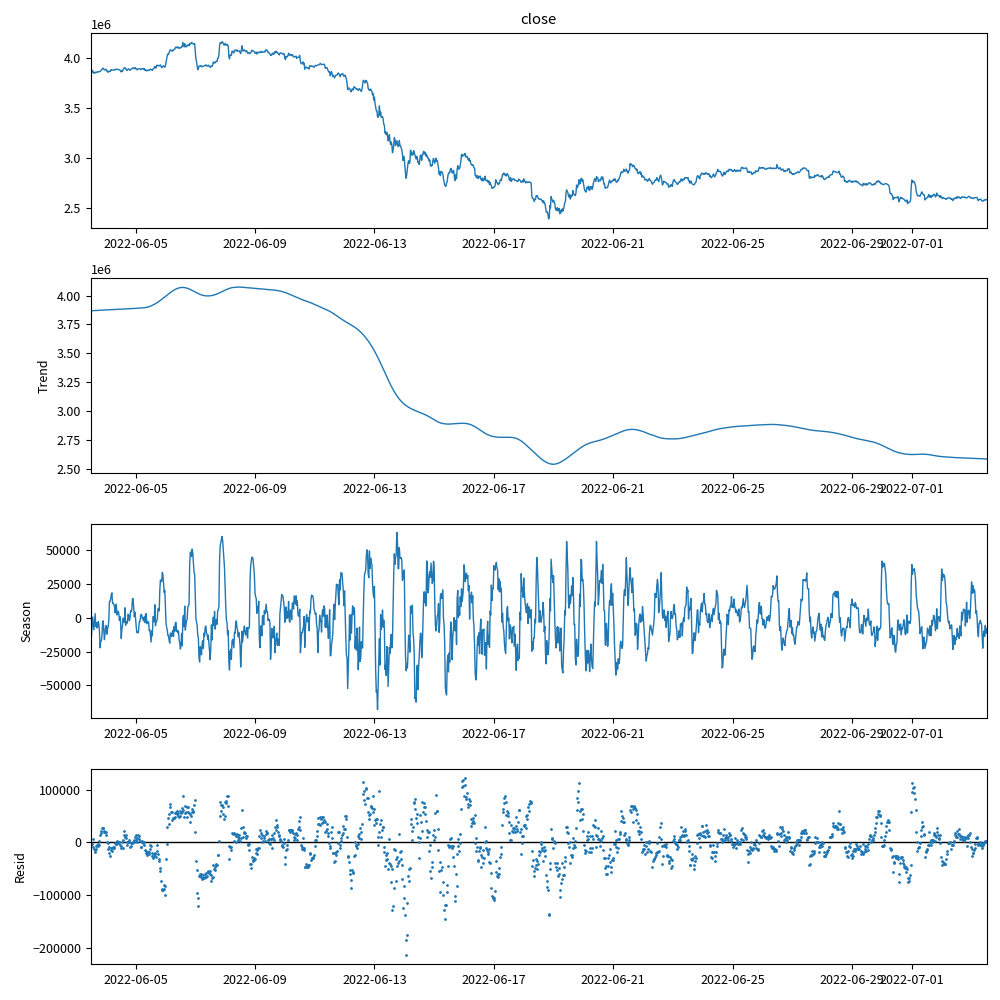
時系列データを分解する
まずは、このサイト でやっているように、時系列データを3つの成分に分解してみます。
- トレンド成分
- 季節成分
- 不規則変動成分
成分分解には、STL (Season-Trend decomposition using LOESS) を使います。
statsmodels.tsa.seasonal.STL 公式ドキュメント
LOESS は locally estimated scatterplot smoothing の略です。
LOESSとは、局所的な区間でデータのばらつきが最も小さくなる線のことを言います。
出典:トレンドライン:LOESS曲線の引き方
from statsmodels.tsa.seasonal import STL # 30分足なので、シーケンスの周期性(period)は24時間x2=48とする。 res = STL(df['close'], period=48).fit() plt.rcParams["figure.figsize"] = (10, 10) plt.rcParams["lines.linewidth"] = 1 plt.rcParams["lines.markersize"] = 1 res.plot() plt.show()
定常性を数値化する
定常性 を数値で判断できるように ADF (Augmented Dickey-Fuller) 検定 を使います。
statsmodels.tsa.stattools.adfuller 公式ドキュメント
from statsmodels.tsa.stattools import adfuller
res = adfuller(df['close'])
adf = {}
adf.update({'adf_test_statistic': res[0]})
adf.update({'p_value': res[1]})
adf.update({'used_lag': res[2]})
adf.update({'n_obs': res[3]})
adf.update({'critical_values': res[4]})
adf.update({'icbest': res[5]})
print(json.dumps(adf, indent=4))
{
"adf_test_statistic": -0.9302950907383377,
"p_value": 0.7778321943839444,
"used_lag": 16,
"n_obs": 1419,
"critical_values": {
"1%": -3.434966750462565,
"5%": -2.8635789736973725,
"10%": -2.5678555388041384
},
"icbest": 32149.22929998816
}
ADF検定の結果を見方を説明したいのですが、十分に理解できていないので他サイトを参考にしてください。
データを加工して、定常性を測る
加工していない生データの BTC_JPY 30分足 の終値のADF検定結果は、上で述べました。
ここでは、終値を加工して定常性の変化を見てみたいと思います。
6つのパターンを見てみたいと思います。
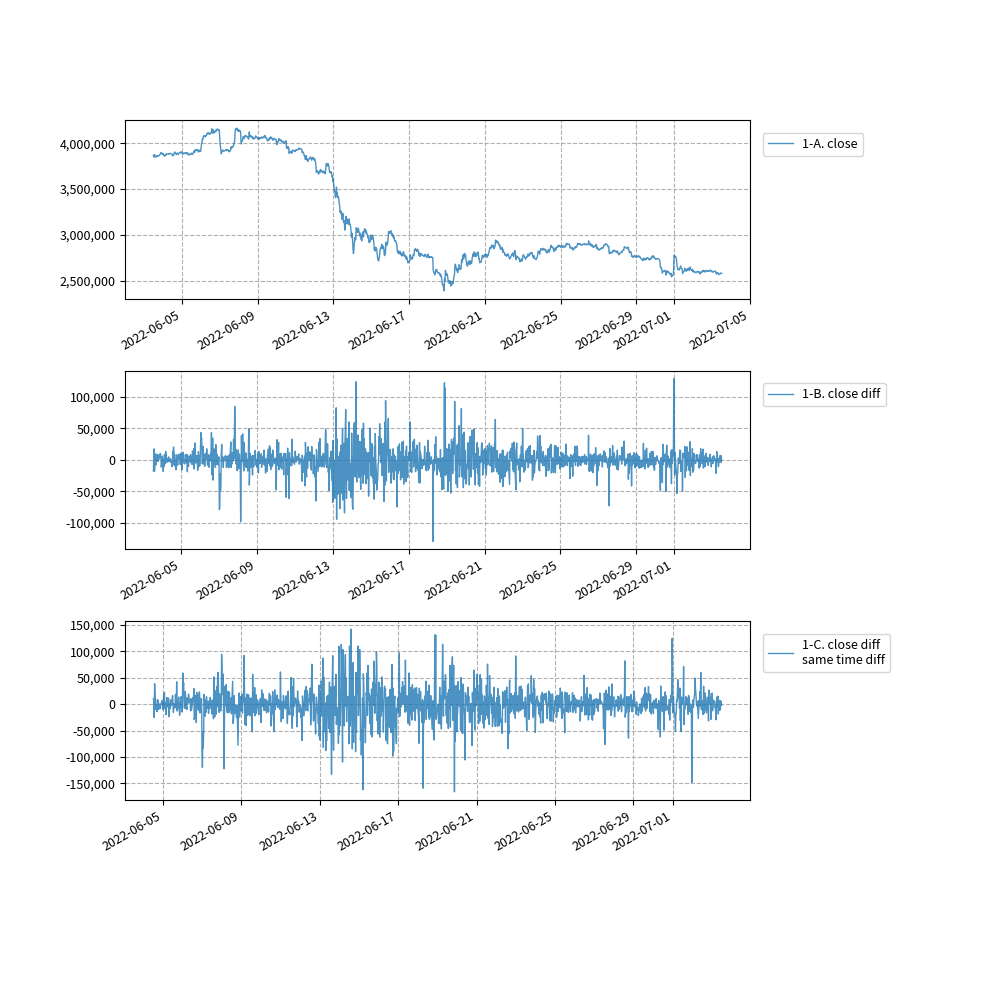
- 1-A. 終値
- 1-B. ひとつ前の終値との差分値
- 1-C. ひとつ前の終値との差分値の、さらに前の同じ時刻との差分値
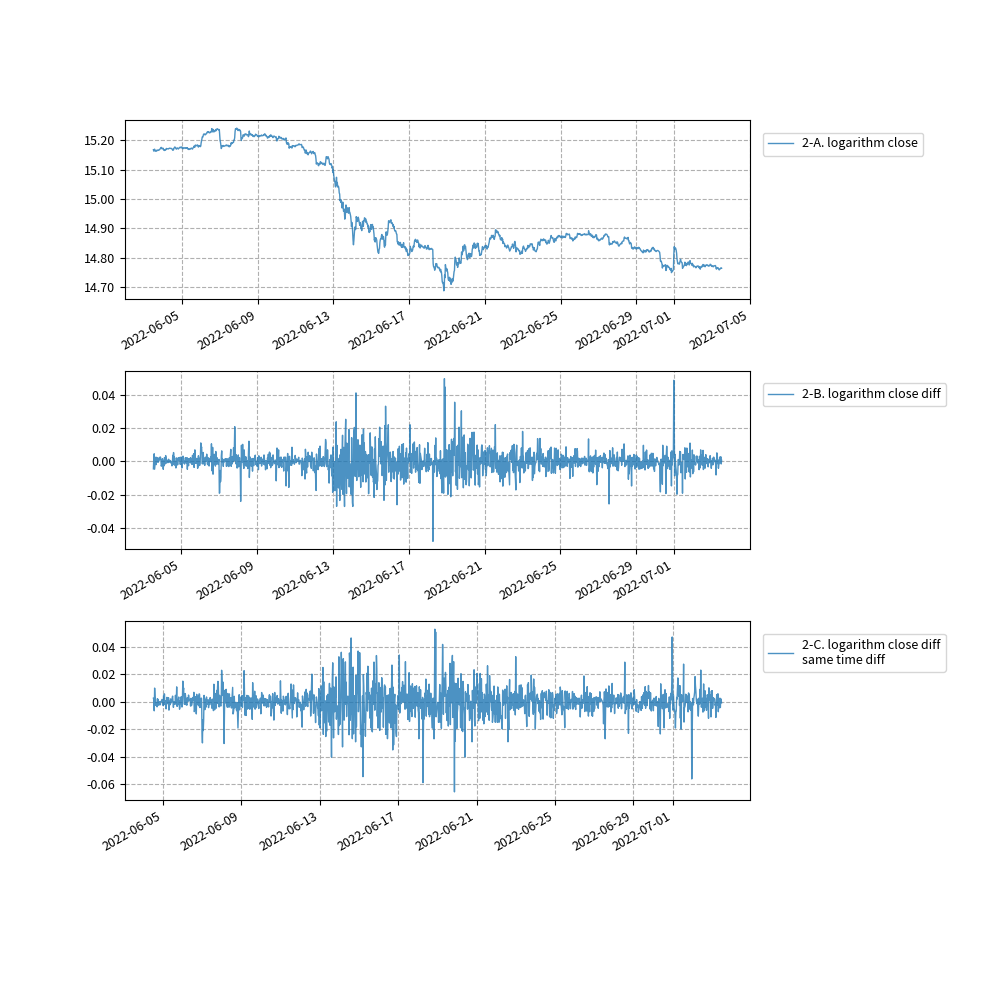
- 2-A. 終値の対数価格
- 2-B. ひとつ前の終値の対数価格との差分値
- 2-C. ひとつ前の終値の対数価格との差分値の、さらに前の同じ時刻との差分値
6つのパターンの計算方法です。
48 は 30分足 の価格だからです。
- 1-A. df[‘close’]
- 1-B. df[‘close’].diff(1).dropna()
- 1-C. df[‘close’].diff(1).dropna().diff(48).dropna()
- 2-A. df[‘close’].apply(np.log1p)
- 2-B. df[‘close’].apply(np.log1p).diff(1).dropna()
- 2-C. df[‘close’].apply(np.log1p).diff(1).dropna().diff(48).dropna()
対数価格については、以下の記事で書きました。
 株価を対数価格で見る
株価を対数価格で見る
ADF検定の結果です。
差分値の検定結果は、すべて定常性がありそうです。
1-A. 終値 ADF test statistic: -0.9302950907 p value: 0.77783219438394435308 critical value 1%: -3.4349667505 critical value 5%: -2.8635789737 critical value 10%: -2.5678555388 1-B. ひとつ前の終値との差分値 ADF test statistic: -9.6515370349 p value: 0.00000000000000014304 critical value 1%: -3.4349667505 critical value 5%: -2.8635789737 critical value 10%: -2.5678555388 1-C. ひとつ前の終値との差分値の、さらに前の同じ時刻との差分値 ADF test statistic: -11.4576346865 p value: 0.00000000000000000001 critical value 1%: -3.4351182380 critical value 5%: -2.8636458244 critical value 10%: -2.5678911386
2-A. 終値の対数価格 ADF test statistic: -1.0490666826 p value: 0.73495060303768677823 critical value 1%: -3.4349929741 critical value 5%: -2.8635905463 critical value 10%: -2.5678617015 2-B. ひとつ前の終値の対数価格との差分値 ADF test statistic: -6.6683210686 p value: 0.00000000465630538516 critical value 1%: -3.4349929741 critical value 5%: -2.8635905463 critical value 10%: -2.5678617015 2-C. ひとつ前の終値の対数価格との差分値の、さらに前の同じ時刻との差分値 ADF test statistic: -8.2412217070 p value: 0.00000000000057101763 critical value 1%: -3.4351391907 critical value 5%: -2.8636550705 critical value 10%: -2.5678960624
ADF検定に使用した値のチャートです。