Adversarial Validationで特徴量をセレクトする

Adversarial Validation

機械学習において、学習時のtrainデータの特徴量 と 評価時のtestデータの特徴量 の 傾向 or 分布 が同じでないと、評価時の予測値がおかしな値になってしまい、学習したモデルを正しく評価できません。

つまり、時系列データを使用して、未来の値を予測するモデルにおいては、未来の特徴量の傾向が、学習時の特徴量の傾向と異なると、正しく未来の値を予測できないということになります。

そこで、Adversarial Validation という手法を用いて、傾向 or 分布 が長期間において変わらない特徴量を選択する ということをします。

参考： Adversarial Validation のやり方
参考： Python: Adversarial Validation について
参考： Kaggleで役立つAdversarial Validationとは
参考： adversarial validationを実装してみた
参考： Adversarial Validation De 特徴量選択

時系列データ

時系列データは、BTC_JPY 1時間足 で、データの期間は 3年間 とします。

                          open high low close volume
timestamp
2019-07-29 12:00:00+00:00 1026674.0 1034294.0 1025061.0 1033584.0 113.48
2019-07-29 13:00:00+00:00 1033584.0 1040461.0 1028040.0 1034620.0 248.96
2019-07-29 14:00:00+00:00 1034212.0 1039848.0 1030073.0 1034321.0 166.42
2019-07-29 15:00:00+00:00 1035125.0 1041500.0 1032000.0 1034572.0 149.19
2019-07-29 16:00:00+00:00 1035034.0 1051424.0 1020000.0 1037977.0 494.75
... ... ... ... ... ...
2022-07-29 08:00:00+00:00 3183988.0 3193435.0 3167129.0 3188818.0 107.35
2022-07-29 09:00:00+00:00 3188238.0 3220000.0 3181137.0 3214454.0 90.94
2022-07-29 10:00:00+00:00 3213802.0 3220419.0 3196197.0 3200178.0 136.18
2022-07-29 11:00:00+00:00 3199257.0 3202975.0 3140773.0 3166649.0 165.72
2022-07-29 12:00:00+00:00 3167178.0 3178041.0 3142757.0 3153638.0 189.84

一時的な目的変数

Adversarial Validation における目的変数は別にあるのですが、ここでは、特徴量の分布をグラフ化するために、一時的な目的変数を設定します。
一時的な目的変数は、BTC_JPY 終値の差分値 とします。
現在の Bar の終値 と 次の Bar の終値 の差分値を算出し、目的変数とします。

# 終値の差分値を算出する。
df['close_diff'] = df['close'].shift(-1) - df['close']

print(df)

                          open high low close volume close_diff
timestamp
2019-07-29 12:00:00+00:00 1026674.0 1034294.0 1025061.0 1033584.0 113.48 1036.0
2019-07-29 13:00:00+00:00 1033584.0 1040461.0 1028040.0 1034620.0 248.96 -299.0
2019-07-29 14:00:00+00:00 1034212.0 1039848.0 1030073.0 1034321.0 166.42 251.0
2019-07-29 15:00:00+00:00 1035125.0 1041500.0 1032000.0 1034572.0 149.19 3405.0
2019-07-29 16:00:00+00:00 1035034.0 1051424.0 1020000.0 1037977.0 494.75 -6977.0
... ... ... ... ... ... ...
2022-07-29 08:00:00+00:00 3183988.0 3193435.0 3167129.0 3188818.0 107.35 25636.0
2022-07-29 09:00:00+00:00 3188238.0 3220000.0 3181137.0 3214454.0 90.94 -14276.0
2022-07-29 10:00:00+00:00 3213802.0 3220419.0 3196197.0 3200178.0 136.18 -33529.0
2022-07-29 11:00:00+00:00 3199257.0 3202975.0 3140773.0 3166649.0 165.72 -13011.0
2022-07-29 12:00:00+00:00 3167178.0 3178041.0 3142757.0 3153638.0 189.84 NaN

特徴量

特徴量を TA-Lib を使って複数用意します。
SMA, ATR, RSI を選びました。

import talib

# SMAを算出する。
df['SMA_24'] = talib.SMA(df['close'], timeperiod=24)

# ATRを算出する。
df['ATR_24'] = talib.ATR(df['high'], df['low'], df['close'], timeperiod=24)

# RSIを算出する。
df['RSI_24'] = talib.RSI(df['close'], timeperiod=24)

df = df.dropna()
print(df.loc[:, ['close', 'close_diff', 'SMA_24', 'ATR_24', 'RSI_24']])

                          close close_diff SMA_24 ATR_24 RSI_24
timestamp
2019-07-30 12:00:00+00:00 1035975.0 1400.0 1.031560e+06 8982.750000 52.035205
2019-07-30 13:00:00+00:00 1037375.0 1457.0 1.031675e+06 8775.635417 53.199128
2019-07-30 14:00:00+00:00 1038832.0 16168.0 1.031863e+06 8604.025608 54.400767
2019-07-30 15:00:00+00:00 1055000.0 -2523.0 1.032714e+06 9211.024541 64.850761
2019-07-30 16:00:00+00:00 1052477.0 -6248.0 1.033318e+06 9116.898518 62.517805
... ... ... ... ... ...
2022-07-29 07:00:00+00:00 3183988.0 4830.0 3.175204e+06 36847.557612 58.163943
2022-07-29 08:00:00+00:00 3188818.0 25636.0 3.178544e+06 36408.326045 58.685995
2022-07-29 09:00:00+00:00 3214454.0 -14276.0 3.182835e+06 36510.604127 61.356686
2022-07-29 10:00:00+00:00 3200178.0 -33529.0 3.186343e+06 35998.578955 59.135355
2022-07-29 11:00:00+00:00 3166649.0 -13011.0 3.187584e+06 37090.388165 54.316126

特徴量の分布

特徴量の分布を見るために、散布図でプロットしてみます。
X軸は、一時的な目的変数として算出した終値の差分値としています。
それに対して、その差分値を叩き出したときの、SMA, ATR, RSI をY軸としています。

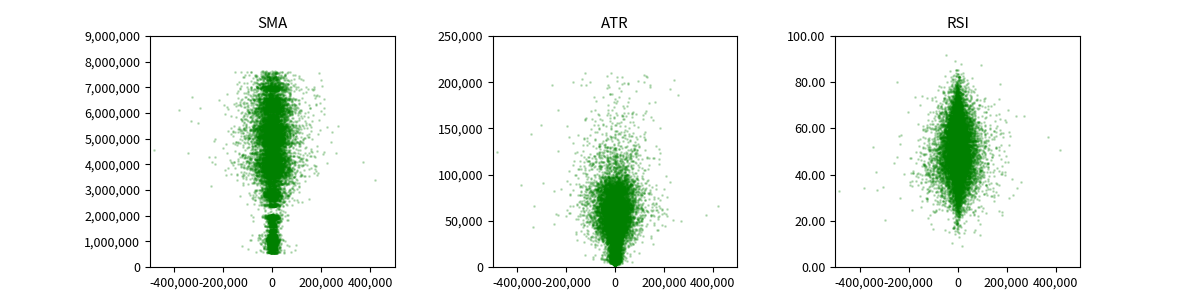
では、このあたりで本題の Adversarial Validation の話に戻します。
時系列データの未来の予測値の精度を上げるためには、特徴量の分布が時間方向にあまりブレないものがいい、ということは想像できると思います。
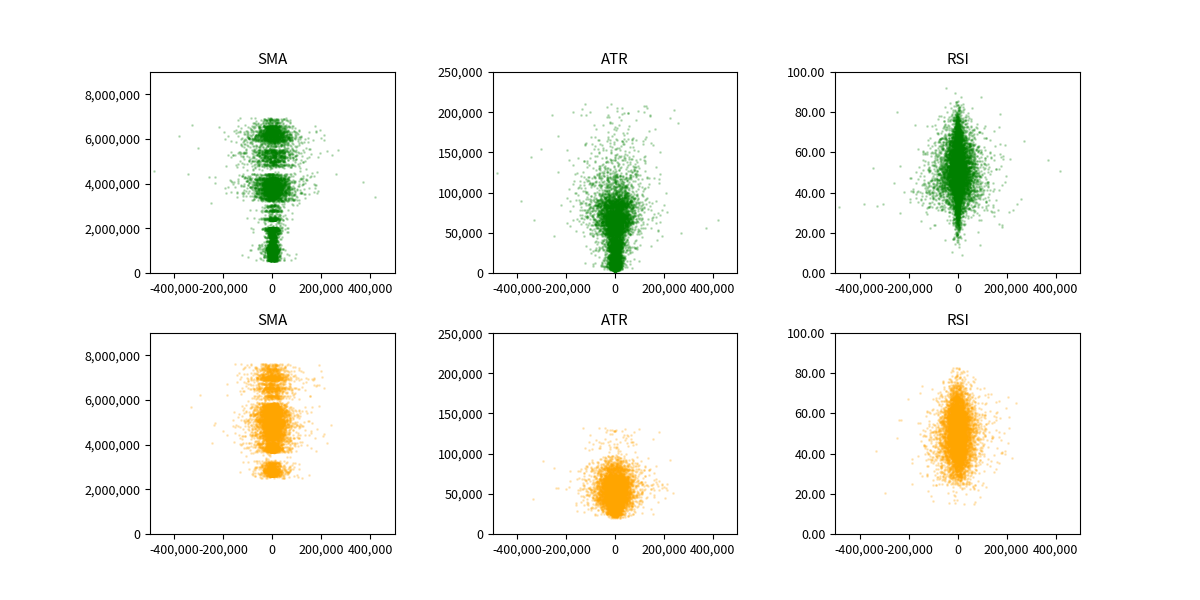
では、今回取り上げた SMA, ATR, RSI の時間方向のブレを散布図で見てみます。
データ期間は3年間なので、前半2年間 と 後半1年間 で色を変えてみます。
前半2年間が緑色で、後半1年間がオレンジ色です。

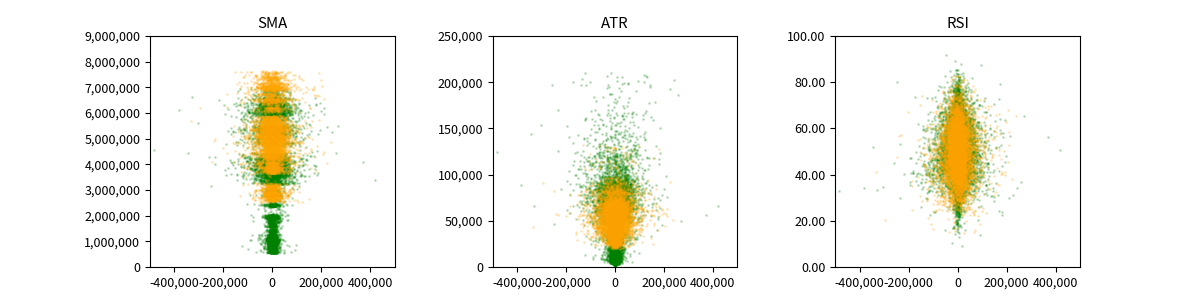
プロットを透過させているのですが、データ量が多すぎて、透過できていないので、違う図にそれぞれプロットしてみます。
パッと見た感じですが、RSI が最も分布に時間的なブレが無いように見えます。
これを Adversarial Validation で明らかにしていきます。

Adversarial Validation

特徴量が時間方向に傾向がブレていない ということを調べるには、期間を分割し、それぞれにラベルを付け、特徴量を使って、そのラベルを分類できるか、という作業を行います。

うまく分類できれば、特徴量の分布が時間方向に依存する要素を含んでいる、ということになります。
うまく分類できなければ、特徴量の分布が時間方向にブレていないことを示唆しています。
つまり、ラベルを分類できない特徴量が、求めている特徴量となります。

では、Adversarial Validation をしていきます。
データを 前半2年間 と 後半1年間 に分割し、それぞれ 0 と 1 のラベルを付けます。

df_a = df[df.index < pd.to_datetime('2021-07-29 12:00:00', utc=True)]
df_b = df[df.index >= pd.to_datetime('2021-07-29 12:00:00', utc=True)]

# 前半2年間に 0 のラベルを、後半1年間に 1 のラベルを付与する。
df_a['y'] = 0
df_b['y'] = 1

# データをつなげる
df = pd.concat([df_a, df_b], axis=0)

                          close close_diff SMA_24 ATR_24 RSI_24 y
timestamp
2019-07-30 12:00:00+00:00 1035975.0 1400.0 1.031560e+06 8982.750000 52.035205 0
2019-07-30 13:00:00+00:00 1037375.0 1457.0 1.031675e+06 8775.635417 53.199128 0
2019-07-30 14:00:00+00:00 1038832.0 16168.0 1.031863e+06 8604.025608 54.400767 0
2019-07-30 15:00:00+00:00 1055000.0 -2523.0 1.032714e+06 9211.024541 64.850761 0
2019-07-30 16:00:00+00:00 1052477.0 -6248.0 1.033318e+06 9116.898518 62.517805 0
... ... ... ... ... ... ..
2022-07-29 07:00:00+00:00 3183988.0 4830.0 3.175204e+06 36847.557612 58.163943 1
2022-07-29 08:00:00+00:00 3188818.0 25636.0 3.178544e+06 36408.326045 58.685995 1
2022-07-29 09:00:00+00:00 3214454.0 -14276.0 3.182835e+06 36510.604127 61.356686 1
2022-07-29 10:00:00+00:00 3200178.0 -33529.0 3.186343e+06 35998.578955 59.135355 1
2022-07-29 11:00:00+00:00 3166649.0 -13011.0 3.187584e+06 37090.388165 54.316126 1

分類器で分類し、特徴量の寄与度を表示します。

from sklearn.model_selection import train_test_split
import lightgbm

x_train, x_test, y_train, y_test = train_test_split(
    df.loc[:, ['SMA_24', 'ATR_24', 'RSI_24']],
    df['y'],
    test_size=0.2,
    random_state=42,
    )

lgbm = lightgbm.LGBMClassifier()
lgbm.fit(x_train, y_train)

accuracy = lgbm.score(x_test, y_test)
print('accuracy:', accuracy)

importance = pd.DataFrame(
    lgbm.feature_importances_,
    index=['SMA_24', 'ATR_24', 'RSI_24'],
    columns=['importance'],
    )
print(importance)

accuracy: 0.9648653809432881

importance
SMA_24 1472
ATR_24 862
RSI_24 666

Adversarial Validation の結果が出ました。
今回の3つの特徴量を使って、分類したときの精度は 96% でした。
良い精度で、前半2年間 と 後半1年間 を分類できてそうです。
その分類にもっとも寄与した特徴量は SMA でした。
つまり、SMA は 前半2年間 と 後半1年間 の分布に最も偏りがある、ということになります。

グラフを目視で判断したときに、RSI の分布が最も時間方向にブレていなさそうと判断しましたが、importance 結果でもそうなっています。

では、SMA を除いた残りの2つの特徴量で分類器にかけてみます。

x_train, x_test, y_train, y_test = train_test_split(
    df.loc[:, ['ATR_24', 'RSI_24']],
    df['y'],
    test_size=0.2,
    random_state=42,
    )

lgbm = lightgbm.LGBMClassifier()
lgbm.fit(x_train, y_train)

accuracy = lgbm.score(x_test, y_test)
print('accuracy:', accuracy)

importance = pd.DataFrame(
    lgbm.feature_importances_,
    index=['ATR_24', 'RSI_24'],
    columns=['importance'],
    )
print(importance)

accuracy: 0.8447584494939852

importance
ATR_24 1415
RSI_24 1585

精度が 84% に落ちました。
分類に寄与していた特徴量 SMA を外したので、想定通りです。
特徴量を2つに減らすと、寄与度が RSI の方が高くなっています。

以上のように、Adversarial Validation を使って、時間方向に分布の偏りがある特徴量を見つけ出し、特徴量のセレクトをしてみましょう。