仮想通貨のボリンジャーバンド幅に定常性はあるのか

定常性のある特徴量

時系列データに定常性を持たせるという記事で、仮想通貨の価格自体には定常性はなく、前日との価格差には定常性がありそうだ、というお話をしました。
仮想通貨の価格予測をするにあたり、他にも定常性を持っている特徴量を探してみたいと思います。
移動平均線やボリンジャーバンドなどは、価格に応じた動きなので、定常性はなさそうです。
でも、それら指標の上下の幅の定常性はどうでしょう？
ちょっと調べてみたいと思います。
高値と安値のそれぞれの移動平均線の幅でもいいですが、今回は、ボリンジャーバンドの上下の幅を調べてみます。

ボリンジャーバンド幅の定常性

データは、BTC_JPY 30分足の2年間分を使用します。
TA-Lib を使って、ボリンジャーバンド幅を算出します。
Windows11にTA-Libをインストール

Python


    import talib
    from talib import MA_Type
    
    # ボリンジャーバンドとバンド幅の算出
    sigmas = [1, 2, 3]
    for sigma in sigmas:
        # ボリンジャーバンドの期間は、短期トレードと考え、10とする。
        BBANDS_upper, BBANDS_middle, BBANDS_lower = \
            talib.BBANDS(df['close'], timeperiod=10, nbdevup=sigma, nbdevdn=sigma, matype=MA_Type.EMA)
    
        # middleはMAみたいなものだから不要。
        df['BBANDS_upper_' + str(sigma)] = BBANDS_upper
        df['BBANDS_lower_' + str(sigma)] = BBANDS_lower
    
        # バンド幅を算出する。
        df['BBANDS_width_' + str(sigma)] = BBANDS_upper - BBANDS_lower

ボリンジャーバンドとバンド幅をグラフ化してみました。
期間が長いと線が潰れてしまったので、最後の方の期間のみをグラフ化しています。

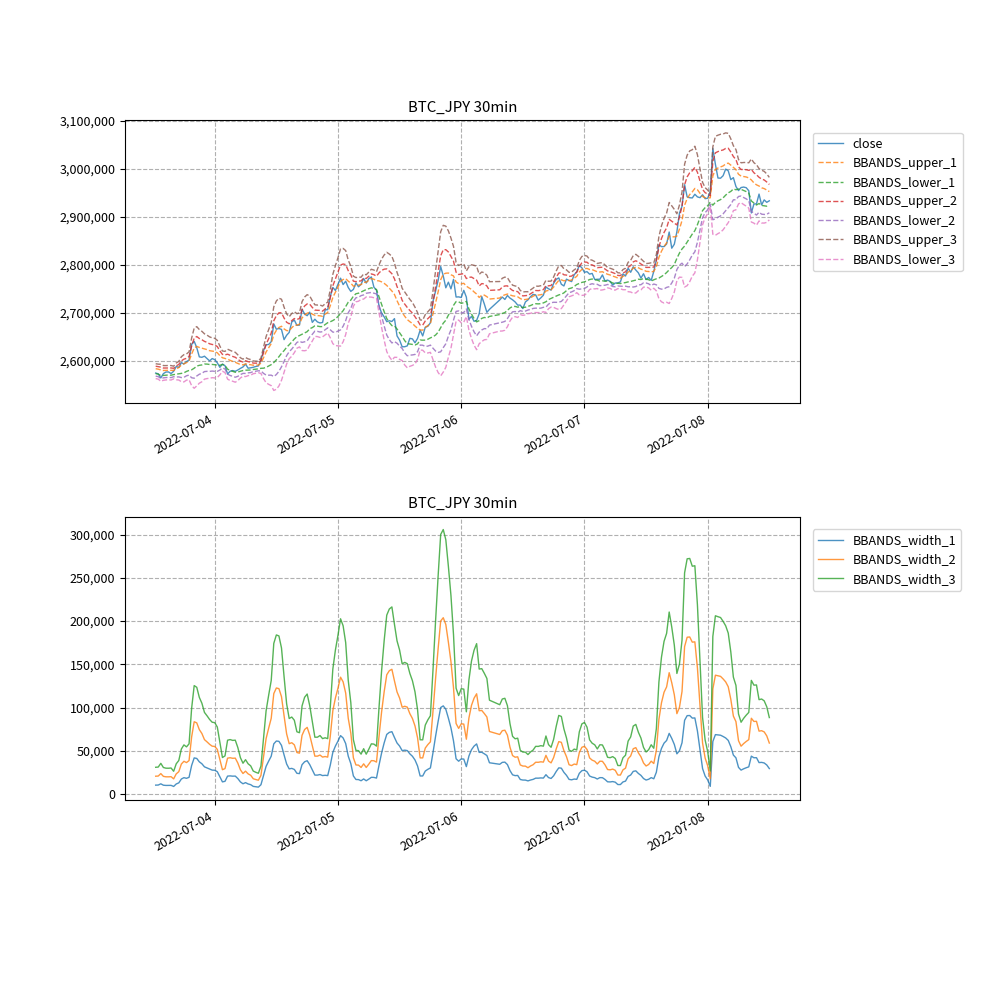
3シグマのバンド幅に関して、トレンド成分、季節成分、不規則変動成分に成分分解してみます。

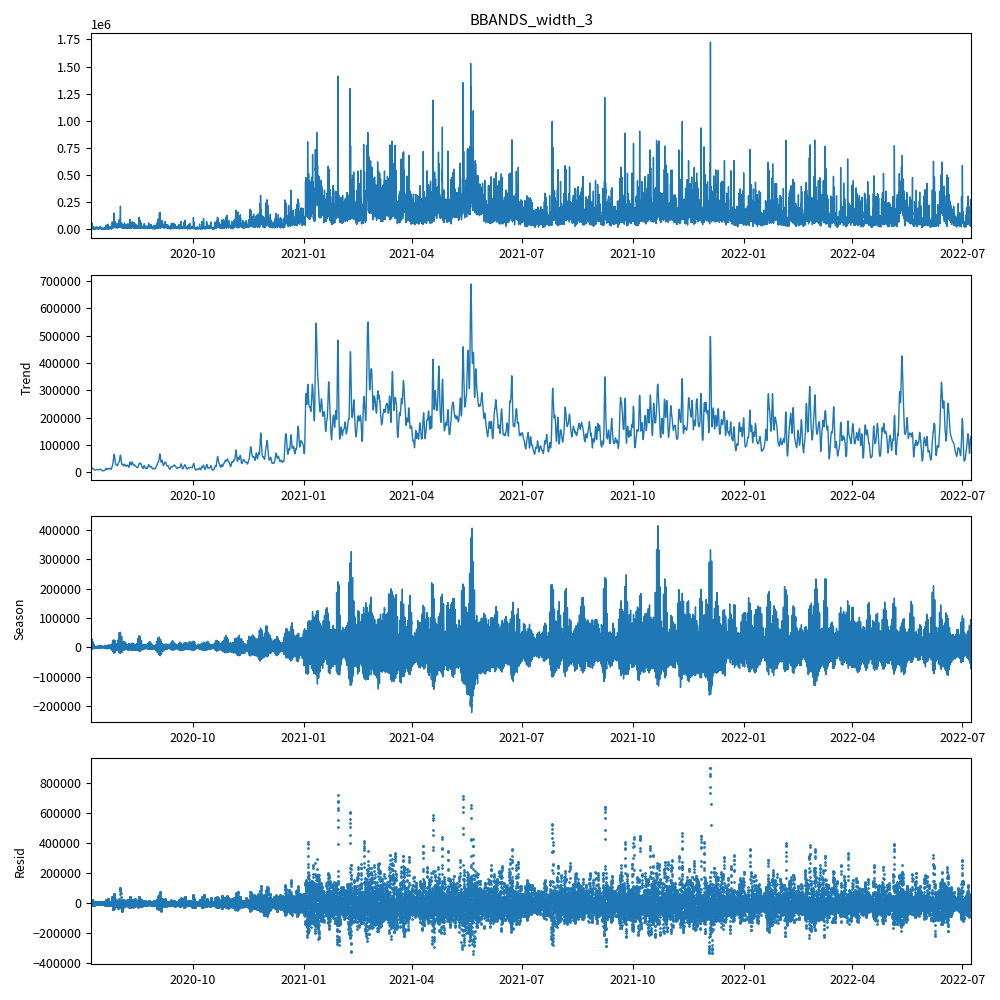
ADF検定をします。
シグマ1, 2, 3 のすべてのバンド幅に定常性がありそうだということがわかりました。

BBANDS_width_1
ADF test statistic: -11.7619751144
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601

BBANDS_width_2
ADF test statistic: -11.7619751144
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601

BBANDS_width_3
ADF test statistic: -11.7619751144
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601

対数価格のボリンジャーバンド幅の定常性

これまで、対数価格についても、このブログで言及してきました。
ついでなので、対数価格でボリンジャーバンドを作成し、そのバンド幅の定常性を見てみたいと思います。

Python


    # 終値の対数価格を算出する。
    df['close log'] = df['close'].apply(np.log1p)
    
    # ボリンジャーバンドとバンド幅の算出
    sigmas = [1, 2, 3]
    for sigma in sigmas:
        # ボリンジャーバンドの期間は、短期トレードと考え、10とする。
        BBANDS_upper, BBANDS_middle, BBANDS_lower = \
            talib.BBANDS(df['close log'], timeperiod=10, nbdevup=sigma, nbdevdn=sigma, matype=MA_Type.EMA)
    
        # middleはMAみたいなものだから不要。
        df['LOG_BBANDS_upper_' + str(sigma)] = BBANDS_upper
        df['LOG_BBANDS_lower_' + str(sigma)] = BBANDS_lower
    
        # バンド幅を算出する。
        df['LOG_BBANDS_width_' + str(sigma)] = BBANDS_upper - BBANDS_lower

対数価格に関しても、ボリンジャーバンドとバンド幅をグラフ化してみます。

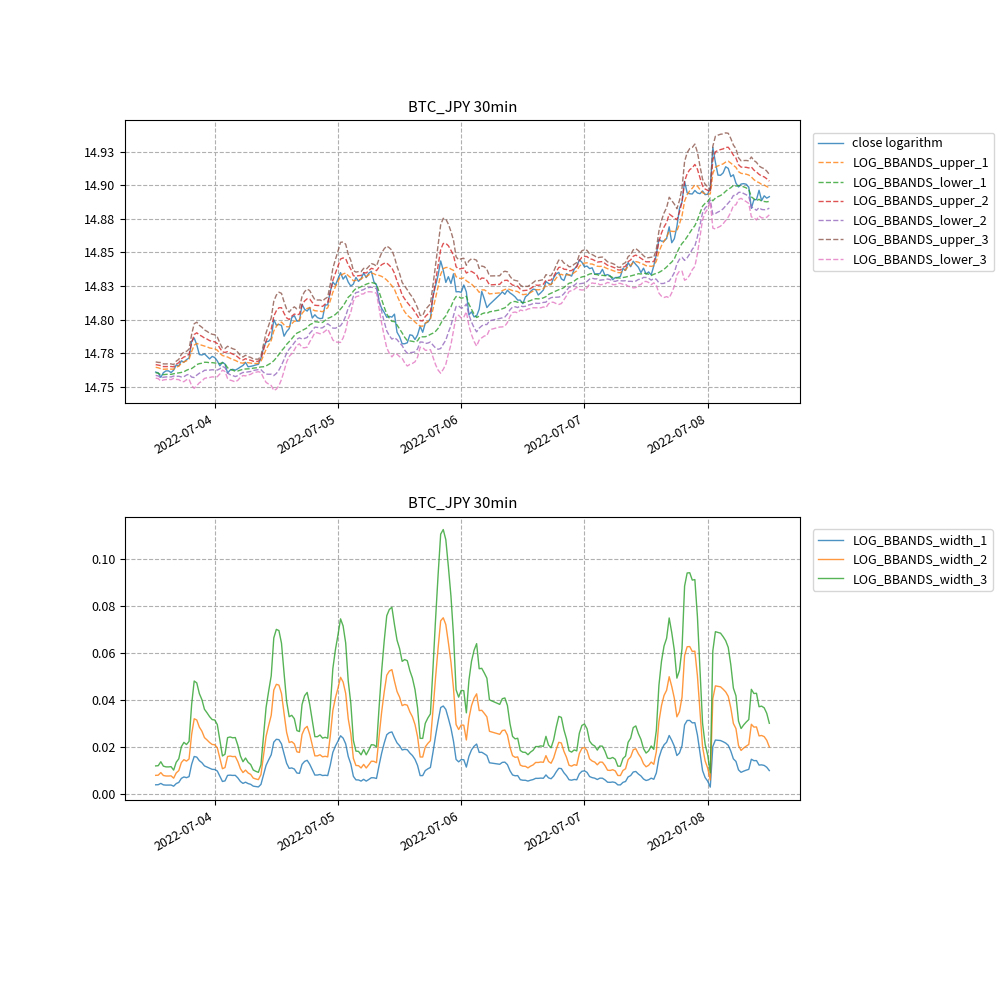
対数価格の3シグマのバンド幅に関して、トレンド成分、季節成分、不規則変動成分に成分分解してみます。
この季節成分が、通常価格と対数価格の違いが分かるグラフになっています。

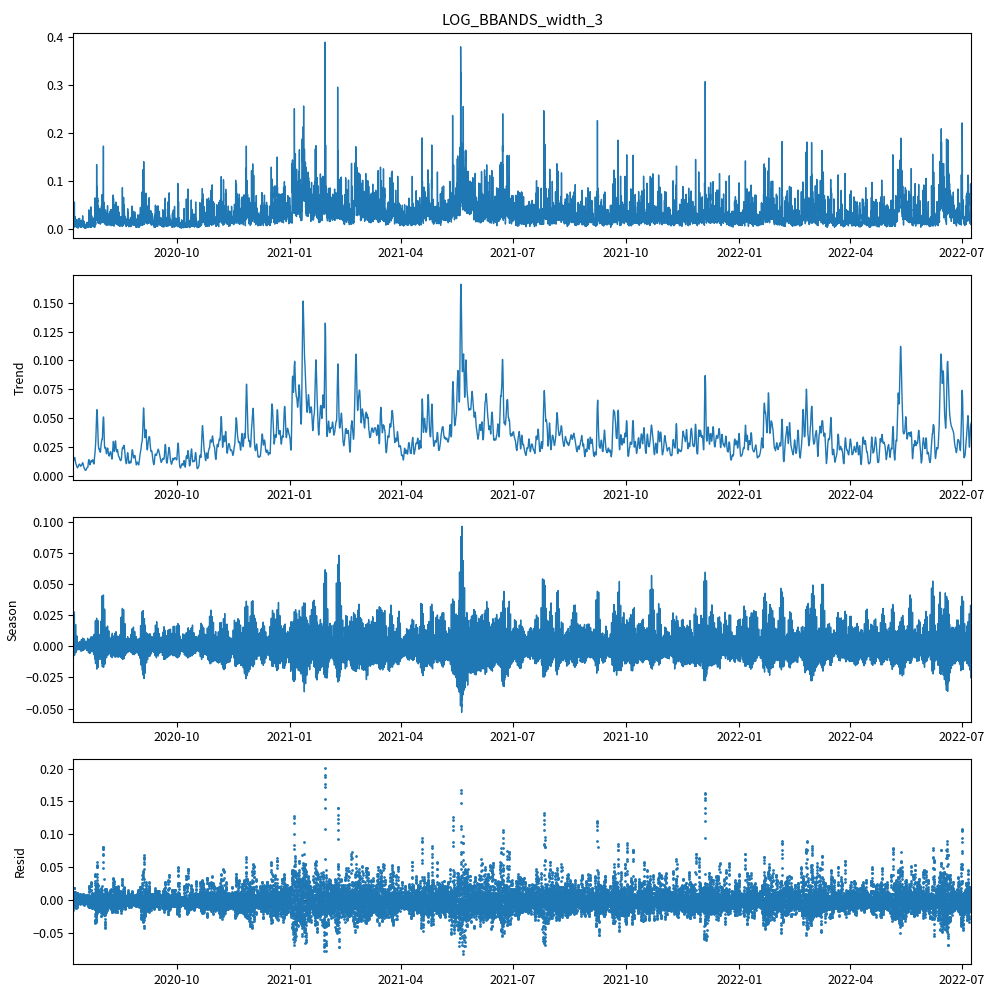
ADF検定をします。
通常価格も対数価格も定常性はありますが、対数価格の方が定常性があると言えそうです。

LOG_BBANDS_width_1
ADF test statistic: -13.6152882199
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601

LOG_BBANDS_width_2
ADF test statistic: -13.6152882199
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601

LOG_BBANDS_width_3
ADF test statistic: -13.6152882199
p value: 0.00000000000000000000
critical value 1%: -3.4305381411
critical value 5%: -2.8616231537
critical value 10%: -2.5668142601