時系列データの価格予測には定常性のある特徴量を使用することが重要であると記事にしました。
 時系列データに定常性を持たせる
時系列データに定常性を持たせる
そこで、移動平均乖離率は価格予測の特徴量となり得るのかを調査します。
移動平均乖離率を算出する
時系列データはビットコイン 30分足を使い、移動平均はSMAではなくEMAを使います。
調査に使用するデータの期間は、2020年7月から2022年7月までの2年間とします。
仮想通貨のOHLCVデータの作成方法は以下の記事を見てください。
 ビットコインのOHLCVデータを生成する
ビットコインのOHLCVデータを生成する
EMA算出にはTA-Libを使います。
 Windows11にTA-Libをインストール
Windows11にTA-Libをインストール
import talib
periods = [10, 25, 75, 200]
for period in periods:
df['EMA_' + str(period)] = talib.EMA(df['close'], timeperiod=period)
df = df.dropna()
print(df)
open high low close volume EMA_10 EMA_25 EMA_75 EMA_200 timestamp 2020-07-12 15:30:00+00:00 986259.0 987664.0 986110.0 986606.0 65.1 987874.6 988946.5 989126.2 993062.9 2020-07-12 16:00:00+00:00 986606.0 987349.0 985356.0 986501.0 127.7 987624.9 988758.4 989057.1 992997.6 2020-07-12 16:30:00+00:00 986501.0 987440.0 986191.0 986309.0 44.2 987385.6 988570.0 988984.8 992931.1 2020-07-12 17:00:00+00:00 986314.0 986463.0 985549.0 985847.0 34.0 987105.9 988360.5 988902.2 992860.6 2020-07-12 17:30:00+00:00 985801.0 986804.0 985400.0 986100.0 36.7 986923.0 988186.6 988828.5 992793.3 ... ... ... ... ... ... ... ... ... ... 2022-07-08 10:00:00+00:00 2926392.0 2954599.0 2917000.0 2946985.0 71.2 2945566.9 2944066.5 2878819.0 2788698.3 2022-07-08 10:30:00+00:00 2947225.0 2947225.0 2920081.0 2924400.0 36.1 2941718.4 2942553.7 2880018.5 2790048.5 2022-07-08 11:00:00+00:00 2923753.0 2941229.0 2912502.0 2934878.0 86.1 2940474.7 2941963.3 2881462.2 2791489.6 2022-07-08 11:30:00+00:00 2935088.0 2943201.0 2926500.0 2929830.0 26.3 2938539.3 2941029.9 2882735.0 2792866.2 2022-07-08 12:00:00+00:00 2929782.0 2948100.0 2923090.0 2933000.0 53.8 2937532.1 2940412.3 2884057.8 2794260.5
移動平均乖離率の計算式です。
移動平均乖離率 = (終値 – 移動平均) ÷ 移動平均
終値を主役ととらえ、移動平均が終値よりも高値になると移動平均乖離率はマイナス値になります。
終値が移動平均からマイナス方向に離れているというイメージとなります。
移動平均乖離率の英訳は、 Moving average deviation rateなので、コード上ではDEV_RATEという略を使用しています。
# 移動平均乖離率の算出
periods = [10, 25, 75, 200]
for period in periods:
df['EMA_' + str(period) + '_DEV_RATE'] = (df['close'] - df['EMA_' + str(period)]) / df['EMA_' + str(period)]
print(df)
open high low close volume EMA_10 EMA_25 EMA_75 EMA_200 EMA_10_DEV_RATE EMA_25_DEV_RATE EMA_75_DEV_RATE EMA_200_DEV_RATE timestamp 2020-07-12 15:30:00+00:00 986259.0 987664.0 986110.0 986606.0 65.10 9.878746e+05 9.889465e+05 9.891262e+05 9.930629e+05 -0.001284 -0.002367 -0.002548 -0.006502 2020-07-12 16:00:00+00:00 986606.0 987349.0 985356.0 986501.0 127.73 9.876249e+05 9.887584e+05 9.890571e+05 9.929976e+05 -0.001138 -0.002283 -0.002584 -0.006542 2020-07-12 16:30:00+00:00 986501.0 987440.0 986191.0 986309.0 44.21 9.873856e+05 9.885700e+05 9.889848e+05 9.929311e+05 -0.001090 -0.002287 -0.002706 -0.006669 2020-07-12 17:00:00+00:00 986314.0 986463.0 985549.0 985847.0 33.95 9.871059e+05 9.883605e+05 9.889022e+05 9.928606e+05 -0.001275 -0.002543 -0.003090 -0.007064 2020-07-12 17:30:00+00:00 985801.0 986804.0 985400.0 986100.0 36.71 9.869230e+05 9.881866e+05 9.888285e+05 9.927933e+05 -0.000834 -0.002112 -0.002759 -0.006742 ... ... ... ... ... ... ... ... ... ... ... ... ... ... 2022-07-08 10:00:00+00:00 2926392.0 2954599.0 2917000.0 2946985.0 71.22 2.945567e+06 2.944067e+06 2.878819e+06 2.788698e+06 0.000481 0.000991 0.023678 0.056760 2022-07-08 10:30:00+00:00 2947225.0 2947225.0 2920081.0 2924400.0 36.08 2.941718e+06 2.942554e+06 2.880018e+06 2.790049e+06 -0.005887 -0.006169 0.015410 0.048154 2022-07-08 11:00:00+00:00 2923753.0 2941229.0 2912502.0 2934878.0 86.06 2.940475e+06 2.941963e+06 2.881462e+06 2.791490e+06 -0.001903 -0.002408 0.018538 0.051366 2022-07-08 11:30:00+00:00 2935088.0 2943201.0 2926500.0 2929830.0 26.29 2.938539e+06 2.941030e+06 2.882735e+06 2.792866e+06 -0.002964 -0.003808 0.016337 0.049041 2022-07-08 12:00:00+00:00 2929782.0 2948100.0 2923090.0 2933000.0 53.83 2.937532e+06 2.940412e+06 2.884058e+06 2.794261e+06 -0.001543 -0.002521 0.016970 0.049652
移動平均乖離率に定常性はあるか
移動平均乖離率のADF検定の結果です。
 時系列データに定常性を持たせる
時系列データに定常性を持たせる
from statsmodels.tsa.stattools import adfuller
# 移動平均乖離率のADF検定
periods = [10, 25, 75, 200]
for period in periods:
res = adfuller(df['EMA_' + str(period) + '_DEV_RATE'])
adf = {}
adf.update({'adf_test_statistic': res[0]})
adf.update({'p_value': res[1]})
adf.update({'used_lag': res[2]})
adf.update({'n_obs': res[3]})
adf.update({'critical_values': res[4]})
adf.update({'icbest': res[5]})
print('\nEMA_{}_DEV_RATE の ADF検定' .format(period))
print('ADF test statistic: {:.10f}' .format(adf['adf_test_statistic']))
print('p value: {:.20f}' .format(adf['p_value']))
for key in adf['critical_values']:
print('critical value {:>3}: {:.10f}' .format(key, adf['critical_values'][key]))
EMA_10_DEV_RATE の ADF検定 ADF test statistic: -26.7986119043 p value: 0.00000000000000000000 critical value 1%: -3.4305391806 critical value 5%: -2.8616236131 critical value 10%: -2.5668145047 EMA_25_DEV_RATE の ADF検定 ADF test statistic: -21.5466534476 p value: 0.00000000000000000000 critical value 1%: -3.4305392135 critical value 5%: -2.8616236277 critical value 10%: -2.5668145124 EMA_75_DEV_RATE の ADF検定 ADF test statistic: -16.4090502792 p value: 0.00000000000000000000 critical value 1%: -3.4305392080 critical value 5%: -2.8616236252 critical value 10%: -2.5668145111 EMA_200_DEV_RATE の ADF検定 ADF test statistic: -11.1465856032 p value: 0.00000000000000000003 critical value 1%: -3.4305392080 critical value 5%: -2.8616236252 critical value 10%: -2.5668145111
すべて定常性はありそうです。
よく考えると、乖離率って 0% から ±N% の間に収まっていてそのレンジを行き来するだけなので、定常性があって当然ということなのかもしれません。
でも、特徴量候補の定常性を数字でしっかりと確認できたことは良かったです。
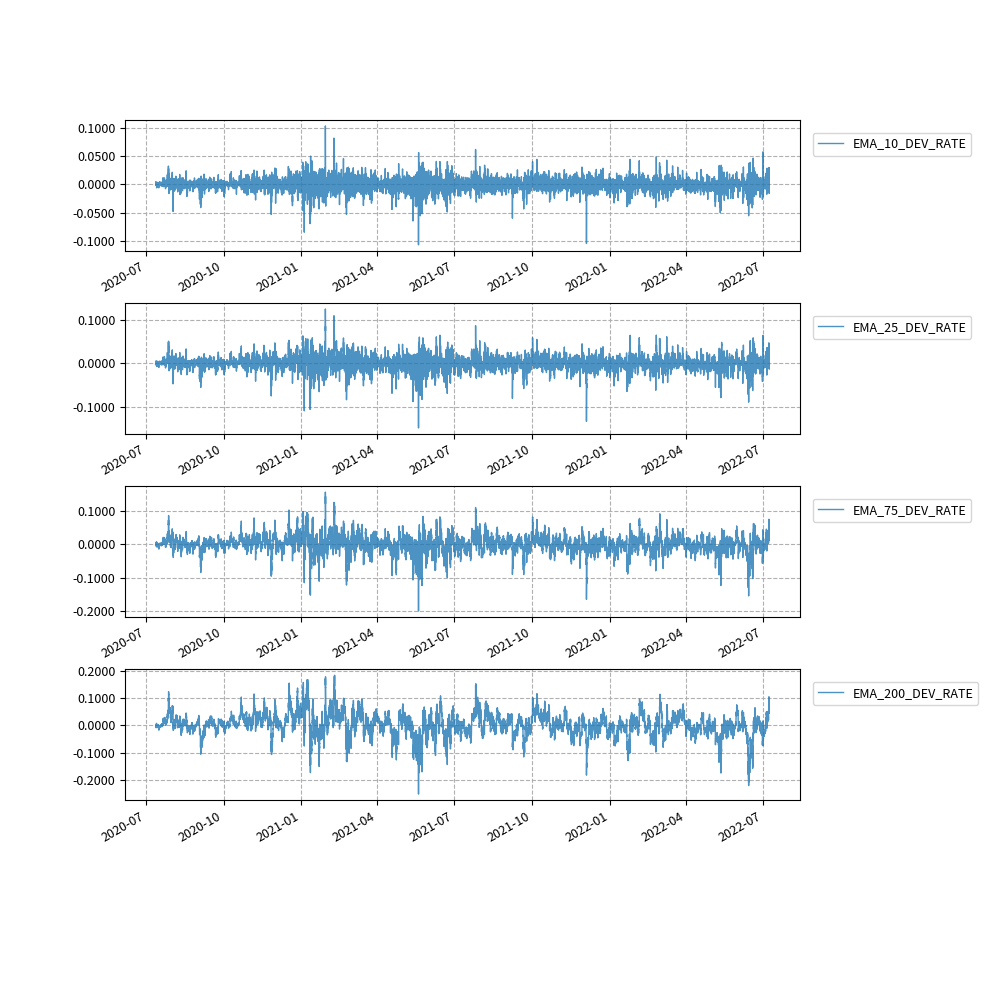
最後に、移動平均乖離率のグラフです。
# 移動平均乖離率のグラフ
fig, axes = plt.subplots(4, 1, figsize=(10, 10))
fig.subplots_adjust(right=0.8, hspace=0.4)
periods = [10, 25, 75, 200]
for period in periods:
graph_id = periods.index(period)
dev_rate_str = 'EMA_' + str(period) + '_DEV_RATE'
df[dev_rate_str].plot(ax=axes[graph_id], alpha=0.8, linewidth=1, label=dev_rate_str)
for ax in axes:
ax.set_axisbelow(True)
ax.grid(axis='both', linestyle='--')
ax.legend(loc="upper left", bbox_to_anchor=(1, 1), borderaxespad=1)
ax.xaxis.label.set_visible(False)
ax.yaxis.set_major_formatter(plt.FuncFormatter(lambda x, loc:"{:,.4f}".format(x)))
plt.show()